Quam?

The Western economy can give thanks to its numerical roots to Pope Sylvester II, who established a bridge between the Arab and Roman worlds, bringing over to Europe (amongst other things) the Hindu-Arabic numeral system. Facing considerable resistance and suspicion, his efforts proved largely fruitless during his lifetime, as various centuries would pass before they took hold, and others such as Fibonacci would receive much of the credit. However, Hindu-Arabic numerals would come to displace onerous Roman numerals and stand behind the rise of Europe as the computational language of economic and scientific growth.

We'll indulge in a broad overview overlooking the clash of two numerical systems. This is a journey that spans two civilizations, of past and future—all through the lens of the remarkable and unlikely life of polymath, proto-humanist, monk, and pope, Gerbert d’Aurillac. As you'll see, Sylvester deserves some credit.

The Roman Empire came to an end in 476 AD, following the deposition of Rome’s last emperor Romulus Augustulus—whose painfully ironic name is an amalgam of Rome’s legendary founder Romulus, and its first emperor Augustus. The disparate states that resulted in its wake continued to use, in different degrees of corruption, its language, laws, customs—and its number system. The latter is made up of fixed integers represented by letters from the Latin alphabet, essentially formed as a ‘base ten’ (decimal) system, and arranged in a tally-like combination.

This structure allows for considerable flexibility in notation, and as a result, there has never been a standard way of arranging the numerals. For instance, Romans were more likely to use VIIII instead of IX to represent "9". Additionally, it could often be confusing to tell the difference between numbers and letters. Consequently, usage in ancient Rome varied greatly, and became downright chaotic in the Middle Ages.

Roman numerals can be very economical in terms of digits—for instance in representing one thousand with one digit (M) instead of four (1000)—perhaps handy when carving them into stone columns. It is for this reason that even today in the fields of accounting and finance, $10M refers to $10,000, while $10MM refers to $1,000,000 (ostensibly as M x M)—confusing to the layman used to seeing $10m refer to ten million. That said, the advantage disappears with less round numbers (i.e. MMXXII for 2022). And yet, in other contexts, references to Greek are used, such as when the layman says ‘10k’ to refer to 10,000 - k referring to the prefix kilo is derived from the Greek word χίλιοι (chilioi), meaning “thousand”.

Ultimately, Roman numerals were made for recordkeeping, not for calculation. They can be added and subtracted with (relative) ease, but are far more cumbersome in multiplication and division. The latter is particularly difficult—making it near impossible to work with infinite series, large numbers, and extremely small numbers—let alone for practitioners to visualize and comprehend.

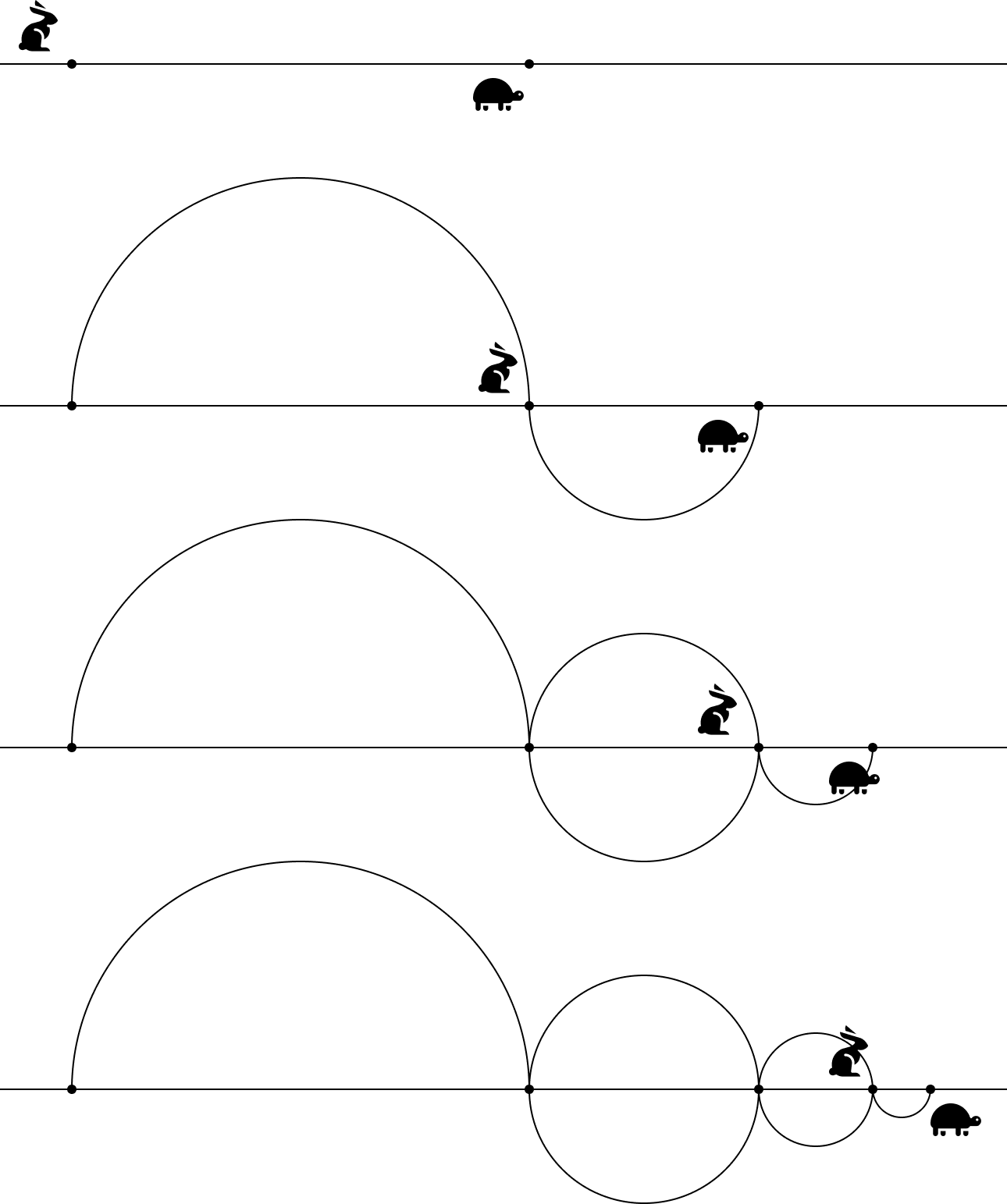
A good example is the Achilles and the tortoise paradox—or as most of us know it, the tale of the hare and the tortoise. The premise is simple. The slower tortoise is given a head start as Achilles runs at twice the tortoise’s speed. The enigma is that Achilles will never quite catch up with the tortoise, as each time he has halved the distance between him and the tortoise, the latter has pottered on, increasing the distance Achilles must run. Our numeral system allows us to intuit and resolve this, whereas through the Roman numeral system, there is no relationship between each division, leaving the thinker thoroughly stumped.

Setting the limitations of the Roman numeral system aside, one must consider the abysmal state of learning as a whole in Europe towards the end of the Early Middle Ages. Numeracy, or the ability for people to interact with numbers and mathematics, had been in steady decline, in line with the collapse of the Roman empire. The ordinary person had little to no contact with mathematics as a subject, and the limited teaching and use it found was almost entirely the preserve of Europe’s academic elite—the clergy. Education had degraded to such an extent that the emperor Charlemagne worried as to whether the clergy even knew enough Latin to interpret the Bible correctly.

The combination of poor numeracy and the limitations of the Roman numeral system made for more mathematical misery. An anecdote of a Norman raid on a French town neatly illustrates this: holding the town hostage, the Normans demanded a tenth of the town’s wealth to keep them from inflicting their worst. Yet no one in the town, nor the Vikings, could actually calculate this figure. So, delegations from each side trudged to a nearby monastery to demand their arithmetic assistance. While impatient Normans sharpened their blades outside, the monks took several days to calculate the sums—likely something that would take a twelve-year-old today half an hour, or minutes with a calculator!

Mathematics, for the very few who were taught it, was seen in the abstract, rather than something to be applied practically. This is largely because the guardians of the few tidbits of mathematical know-how that remained (the clergy) saw numbers as serving a religious purpose. As far as most clerics were concerned, its use was in the calculation of the accurate timing of Easter, around which all other religious feasts were arranged—and in trying to place the Apocalypse. So critical was the issue of establishing annual religious feast days that it led to the creation of an entire branch of mathematics called computus. To the modern mind, the arithmetic multiplications involved here were straightforward, but without Arabic numerals, it would prove hellishly complicated. This led to creation of a manual finger-based method to help with basic arithmetic calculations—a 'form of sign language equivalent to doing the Macarena while juggling eggs'. Even these arithmetic aids were unlikely to have made his task much easier, with only the Roman numeral system to work with.

As such, those that could put mathematics to practical use had little exposure to it. Traders were the obvious beneficiaries of a working numerical knowledge. They recorded their data using Roman numerals, and many used a fairly elaborate fingers procedure, similar to the one pictured above. This meant that they could make simple calculations, but could not explain how they had arrived at their answers. Even the abacus, of great value to merchants in calculating transactions, had been forgotten over the years.

While clergymen, Frankish tax collectors, and Venetian merchants engaged in ritual gnashing of teeth over simple arithmetic—and the rest of Christendom failed to count their own fingers—the Islamic world stood at its apex. Basking in the glow of its Golden Age, it was its time’s most advanced civilization.

Baghdad, with over a million inhabitants, was the largest city in the world during much of this period, at a time when the populations of Paris and London hovered around 20,000. Baghdad contained the renowned House of Wisdom, described by historian Eamonn Garon as having the reputation of ‘Harvard, Yale, Oxford, Cambridge, and some more.’ It boasted the largest collection of books in the world by the 9th Century, with over a million volumes.

Among its many distinguished scholars stood its chief astronomer and head librarian, the inimitable Muhammad al-Khwarizmi. The Persian polymath and father of algebra, al-Khwarizmi’s very name gave rise to the term ‘algorithm’. Though first invented by Indian scholars between the 1st and 4th Centuries and slowly spreading westwards, it was al-Khwarizmi’s On the Calculation with Hindu Numerals (written ~820 AD) that brought the Hindu-Arabic numeral system into general use in the Muslim world. Through this medium, it fanned out to the other great cities of the Muslim world, including Damascus and Cairo, through Morocco, and to Al-Andalus (Muslim Spain). The latter was dominated by the city of Cordoba, itself Europe’s largest city at the turn of the millennium, rivaling Baghdad as a center of learning. The term algebra itself comes from the title of his book. The word al-jabr meaning ‘completion’ or ‘rejoining’.

It is at this frontier in the Iberian Peninsula, between Muslim Al-Andalus to the South, and Christian Europe to the North, where our protagonist Gerbert makes an entrance. Born a peasant in France, he joined the Church and took monastic vows. His keen mind was eventually recognized, which led to him being sent to learn mathematics in Catalonia. Bordering Al-Andalus, it was here where he was first exposed to the Muslim world and its ideas. The stories of Spanish Christians living under Muslim rule (known as ‘Mozarabs’) sparked Gerbert’s veneration of the Arabs, and stoked his passion for mathematics.

Though questioned by historians, it is traditionally held that Gerbert, despite being a Catholic clergyman, even studied at the Muslim Al Quaraouiyine university in Morocco, known as the oldest extant university in the world. Regardless as to whether he physically studied in Morocco or Spain, Gerbert absorbed knowledge with an incredible appetite. Besides mathematics, he studied engineering, mechanics, astronomy, and other sciences known to the Arabs. Founded in 859 AD, years before Europe’s oldest, the University of Bologna, was founded in 1088.

This intellectual foundation set him on the path to becoming one of the most noted scientists and academics of his time. He so impressed and delighted Pope John XIII with his mathematical prowess in 970 that the pontiff presented him to Holy Roman Emperor Otto I, who entrusted him with the instruction of the royal heir, Otto II. Amidst being drawn into the intricate and dangerous game of high politics between the Holy Roman Empire, the Papal States, and France, which saw his standing wax and wane, he was also credited with various intellectual achievements—creating the most advanced hydraulic-powered pipe organ in Rheims, numerous theological treatises, and as an early proponent of the astrolabe.

His ascension to the papacy in 999 as the first French pontiff proved equally remarkable given almost exclusively Italian papal predecessors. Choosing the pontifical name Sylvester II, Gerbert set upon a vigorous agenda of reform among the clergy. His position also provided him a platform from which to continue his attempts to spread mathematics, and learning as a whole.

Gerbert was no doubt ahead of his time—his nonconformity to medieval patterns made him many enemies during his life and after his death. As an ambitious Frenchman with a reforming zeal, and in league with the Holy Roman Emperor, he earned the enmity of Roman nobility and Italian high clergy, as well as the mistrust of the Roman populace. Subsequently, the Roman populace revolted in 1001, with Sylvester II and the Emperor forced to leave Rome. Though he returned in 1002, he would never gain the trust of these groups.

This continued after his death in 1004, where a number of peculiar legends arose to explain his out-of-the-ordinary intellectual abilities, and his ascension from obscure beginnings to the throne of St Peter. One of these held that Gerbert had secured the papacy by playing dice with the Devil, while another held that Gerbert learnt the art of divination in Spain from a wizard from whom he stole a book full of secrets, and a third that he had constructed a bronze head automaton that answered yes or no questions. So pervasive were the clouds that hung over Sylvester II that six centuries later, Pope Innocent X exhumed his body in 1634 to see if he had any Hindu-Arabic numerals on himself, only to confirm that he did not, in fact.  

Ultimately, Sylvester II was unsuccessful in bringing Hindu-Arabic numerals into the mainstream, as can be seen in the persistence of Roman numerals right into the 14th and 15th centuries. He was met with indifference, suspicion, or active resistance across a number of sources, and ironically from those who could benefit the most from the change, such as the merchant class.

Nevertheless, Hindu-Arabic numerals did eventually displace their Roman counterparts. Their advantages soon became apparent—making multiplication and division nearly as easy as addition, already a staggering achievement. Positional notation and the use of zero proved immensely useful. The widespread adoption of this new system eventually affected nearly all sectors. The vastly more efficient arithmetic system significantly facilitated calculation of the mathematical tables used in surveying, architecture, construction, navigation, and astrology, and the keeping of financial records—all of which contributed to the rise of exploration and the growth of capitalism that would characterize the Renaissance. Characters such as Leonardo of Pisa, known to us as Fibonacci, received the bulk of the credit for popularizing the number system, notably through his 1202 book Liber Abaci (‘The Book of Calculation’).

More fundamentally, banking and accounting could hardly have developed without a numeral system that permits the expression of large quantities in a compact form, and a mechanism for the easy calculation of interest. Whereas previously, merchants were limited to performing simple transactional calculations using their (impressively advanced) finger method or an abacus (once reintroduced by Sylvester, of course), the sort of record-keeping required by bankers who accepted funds on deposit, and then lent or invested the money, required a lasting and compact notation, which the Hindu-Arabic system provided. One can hardly imagine what coding with roman numerals would have looked like!

We can see Sylvester as a forerunner, ahead of his time, who paved the way for the eventual spread of numeracy and learning. Restricted by the blinkers of the backwards society he operated in, his intellect and humanism stuck out like a sore erudite thumb. Even rising to the highest position at the head of the most powerful institution in Europe did not help him or legitimize his ideas, but only further entrenched suspicion and resentment across a number of groups. The august historian Hallam wrote that in the 500 years between the 6th and 11th centuries, Gerbert AKA Sylvester was one of only two serious intellectual lights that shone in Europe. It is precisely the context of Europe’s intellectual deficit and inflexibility that shows our protagonist to be so remarkable.

Similar parallels might be drawn with other waves of computing languages that have revolutionized computing since then. Take for instance, the introduction of C—born from the work of Dennis Ritchie at Bell Laboratories in 1972. As the original “high-level” programming language that replaced assembly language (and the rote punching of paper tape cards encoded with hand-written code that came before), C became the language of Unix and the de facto standard across the budding computer industry. Today, it’s considered to be the language that made nearly all languages that came after it possible. It makes one wonder if there are similar quantum leaps in innovation still in store, waiting to be unlocked by new languages that enable the conceptualization and execution of computation in novel ways.

Ultimately, we remember Sylvester II as one of Europe’s greatest teachers, and an early bridge allowing the interchange of knowledge from East to West, which would in due time bring Europe from the Dark Ages, seated on the ashes of its former Roman glory, and at the edge of the civilized world, to the world’s economic center for centuries to come, and the jumping point for an economic system that spans the globe today.